Today

• Point estimates vs interval estimates

• Confidence intervals

• t-distribution

What stats is about (yet again)

• We want to know about the world (population)

• We can only get data from samples

• We calculate statistics on samples and use them to estimate the values in population

• Statistics is all about making inferences about populations based on samples

• If we could measure the entire population, we wouldn't need stats!

Point estimates

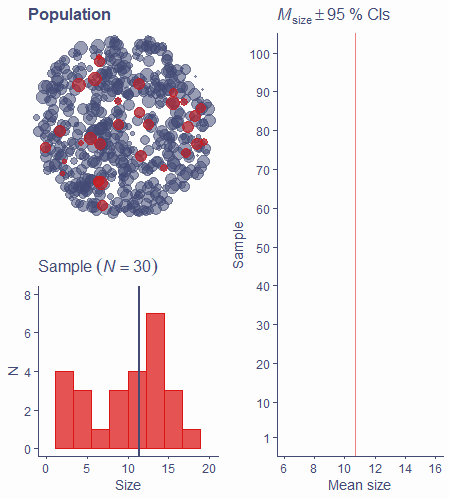
• You've heard of the sample mean, median, mode

• These are all point estimates - single numbers that are our best guesses about corresponding population parameters

• Measures of spread (SD, ${\sigma }^2$, etc.) are also point estimates

• Even relationships between variables can be expressed using point estimates

Point estimates

Accuracy and uncertainty

• Sample mean $\overline{x}$ is the best estimate $\hat{\mu }$ of population mean but means of almost all samples differ from population mean $\mu$

• Same is true for any point estimate

• SE of the mean expresses the uncertainty about the estimates of the population mean

• SE can be calculated for other point estimates, not just the mean

• We can quantify uncertainty around point estimates using interval estimates

Interval estimates

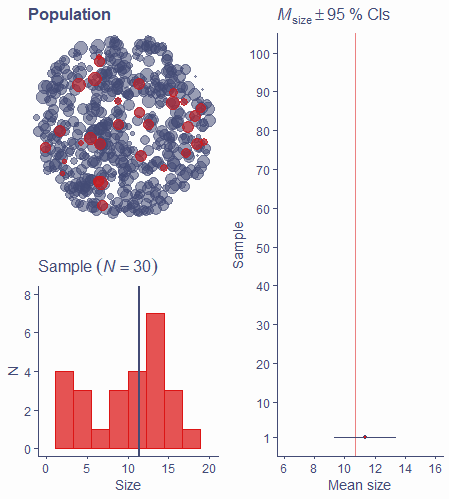
• In addition to estimating a single value, we can also estimate an interval around it

• e.g., mean = 4.13 with an interval from −0.2 to 8.46

• Interval estimates communicate the uncertainty around point estimates

• There are different kinds of interval estimates

  • Important: confidence intervals

Confidence interval

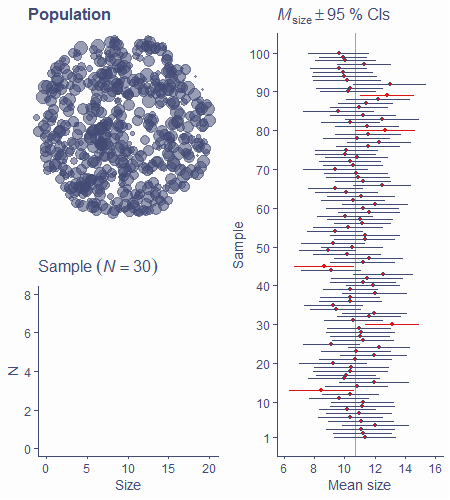
• We can use SE and the sampling distribution to calculate a confidence interval (CI) with a certain coverage, e.g., 90%, 95%, 99%...

• For a 95% CI, 95% of these intervals around sample estimates will contain the value of the population parameter

• Let’s see an example

Confidence interval

• Population of circles of different sizes

Confidence interval

• Sample from population, estimate mean size

Confidence interval

• Calculate the 95% CI around the mean

Confidence interval

• Lather, rinse, repeat...

Confidence interval

• ~5% don't contain population mean = 95% coverage

How is it made?

• Easy if we know sampling distribution of the mean

• 95% of sampling distribution is within ±1.96 SE

• 95% CI around estimated population mean is mean ±1.96 SE

How is it made?

• Sampling distribution of the mean is normal (as per CLT)

• Middle 95% of the sample means lie within ±1.96 SE

• We use the same 1.96 SE to construct 95% CI around mean

How is it made?

• Sampling distribution is, however, not known!

• It can be approximated using the t-distribution and s and N

t-distribution

• Symmetrical, centred around 0
• Its shape changes based on degrees of freedom
• As shape changes, so do proportions (unlike with normal)
• In standard normal, middle 95% of data lie within ±1.96
• In t-distribution, this critical value changes based on df

t-distribution

• t-distribution crops up in many situations

• Always has to do with estimating sampling distribution from a finite sample

• How we calculate number of df changes based on context

  • Often has to do with N, number of estimated parameters, or both

  • In the case of sampling distribution of the mean, df = N − 1

Back to CI

• 95% CI around estimated population mean is mean ±1.96 SE if we know the exact shape of sampling distribution

  • We don't know the shape so we approximate it using the t-distribution

• We need to replace the 1.96 with the appropriate critical value for a given number of df

• For N = 30, t_crit(df=29) = 2.05

qt(p = 0.975, df = 29)

## [1] 2.04523

Back to CI

• 95% CI around the mean for a sample of 30 is $\overline{x}\pm 2.05\times SE$

• $\widehat{SE}=\frac{s}{\sqrt{N}}$

• $95\%CI=Mean\pm 2.05\times \frac{s}{\sqrt{N}}$

• To construct a 95% CI around our estimated mean, all we need is

  • Estimated mean (i.e. sample mean, because $\hat{\mu }=\overline{x}$)
  • Sample SD (s)
  • N
  • Critical value for a t-distribution with N − 1 df

CIs are useful

• Width of the interval tells us about how much we can expect the mean of a different sample of the same size to vary from the one we got

• There's a x% chance that any given x% CI contains the true population mean

• CAVEAT: That's not the same as saying that there's a x% chance that the population mean lies within our x% CI!

• CIs can be calculated for any point estimate, not just the mean!

Remember this?

Remember this?

Take-home message

• Our aim is to estimate unknown population characteristics based on samples
• Point estimate is the best guess about a given population characteristic (parameter)
• Estimation is inherently uncertain
  • We cannot say with 100% certainty that our estimate is truly equal to the population parameter
• Confidence intervals express this uncertainty
  • The wider they are, the more uncertainty there is
  • They have arbitrary coverage (often 50%, 90%, 95%, 99%)
• CIs are constructed using the sampling distribution
  • True sampling distribution is unknown, we can approximate it using the t-distribution with given degrees of freedom
• CIs can be constructed for any point estimate
• For a 95% CI, there is a 95% chance that any given CI contains the true population parameter