In this tutorial, you’ll get started working with the linear model. The goal of this tutorial is to get a feel for the equation of a line and the basic structure of the lm() function. We’ll be spending a lot of time on linear models, so just focus on getting the basics down for now.

Setting Up

All you need is this tutorial and RStudio. Remember that you can easily switch between windows with the Alt + ↹ Tab (Windows) and ⌘ Command + ⇥ Tab (Mac OS) shortcuts.

Task 1

Create a new week_08 project and open it in RStudio. Then, create two new folders in the new week_08 folder: r_docs and data. Finally, open a new R Markdown file and save it in the r_docs folder. Since we will be practising reporting (writing up results), we will need R Markdown later on. For the tasks, get into the habit of creating new code chunks as you go.

Task 2punk!

Add and run the command to load the tidyverse package in the setup code chunk.

library(tidyverse)

The Linear Model

Let’s start with a refresher to get warmed up. In the lecture we learned about the equation of a line, a very important equation that we will be using again and again.

This equation has the following elements:

• \(y\): The value of the outcome
• b₀: the intercept, or value of the outcome when the predictor is 0
• b₁: the slope, or change in the outcome for each unit change in the predictor
• x₁: the predictor

These definitions are important for you to know, but if they don’t make a lot of sense at the moment, don’t worry - that’s what this tutorial is for. We’ll start by getting a handle on what the b-values do first, and then we’ll move on to creating a linear model with the familiar gensex dataset to get some practice using these values.

Using the Equation

Before we jump into the data, let’s have a go practicing with the model itself and getting the hang of how it works. To do this, we’ll use the beautiful interactive visualisation below, courtesy of Milan.

Task 3punk!

Spend a minute playing with the visualisation and moving both sliders to get the hang of how it works. Then try out the quiz questions below.

Well done so far. You can keep playing with the visualisation as much as you like - it will help a lot if you can understand how these values work in the linear model equation.

Flatlining

Before we move on, let’s take a look at a special scenario. Move or reset the sliders so that the line is perfectly horizontal, then answer the following questions.

Now that we have a sense of how the b-values in the linear model work, let’s move on to looking at some data. Remember that you can always come back to the visualisation if you’d like to practice with the equation more.

lm() in R

Let’s have another look at the gensex data we’ve been working with all term. We’ve only had a look at a few variables thus far, but there’s lots more interesting info here!

Creating the Model

Task 4punk!

Read in the gensex data, using the link below.

Link: https://and.netlify.app/datasets/gensex_2022.csv

gensex <- readr::read_csv("https://and.netlify.app/datasets/gensex_2022.csv")

This time we’ll use some different variables. I’ll be using romantic_freq`` andsexual_freq`, which are ratings of how frequently the participants experience romantic and sexual attraction respectively. A higher score indicates higher frequency.

Task 5Prog-rocK

What do you think the relationship between your two variables will be? Take some notes in your RMarkdown document. Consider:

• What direction will the relationship be in?
  • Will it be a positive or negative relationship?
  • What would this look like in the linear model?
• How strong will the relationship be?
  • What will it look like for the relationship to be stronger or weaker?

Task 6

Run the linear model with the following steps.

Task 6.1punk!

Write the formula for lm(), using frequency of romantic attraction as the predictor and frequency of sexual attraction as the outcome.

Task 6.2punk!

Use the lm() function to create a linear model with these variables and save it as freq_lm.

## with pipe
freq_lm <- gensex %>% 
  lm(sexual_freq ~ romantic_freq, data = .)

## without pipe

freq_lm <- lm(sexual_freq ~ romantic_freq, data = gensex)

Interpreting the Model

Call the freq_lm object and use the output to answer the following questions. Round all your answers to 2 decimal places.

Task 7Prog-rocK

In your RMarkdown document, write the equation of the linear model for this analysis.

freq_lm

Call:
lm(formula = sexual_freq ~ romantic_freq, data = gensex)

Coefficients:
  (Intercept)  romantic_freq  
       3.3814         0.4682  

Task 8

In your RMarkdown document, write down your interpretation of the b₁ value you obtained. What does it tell you?

Task 9

Move the sliders in the interactive visualisation above to set the visualisation to the same values from your model. Is this the strength and direction of the relationship you predicted? Write down your thoughts in your RMarkdown.

Task 10Prog-rocK

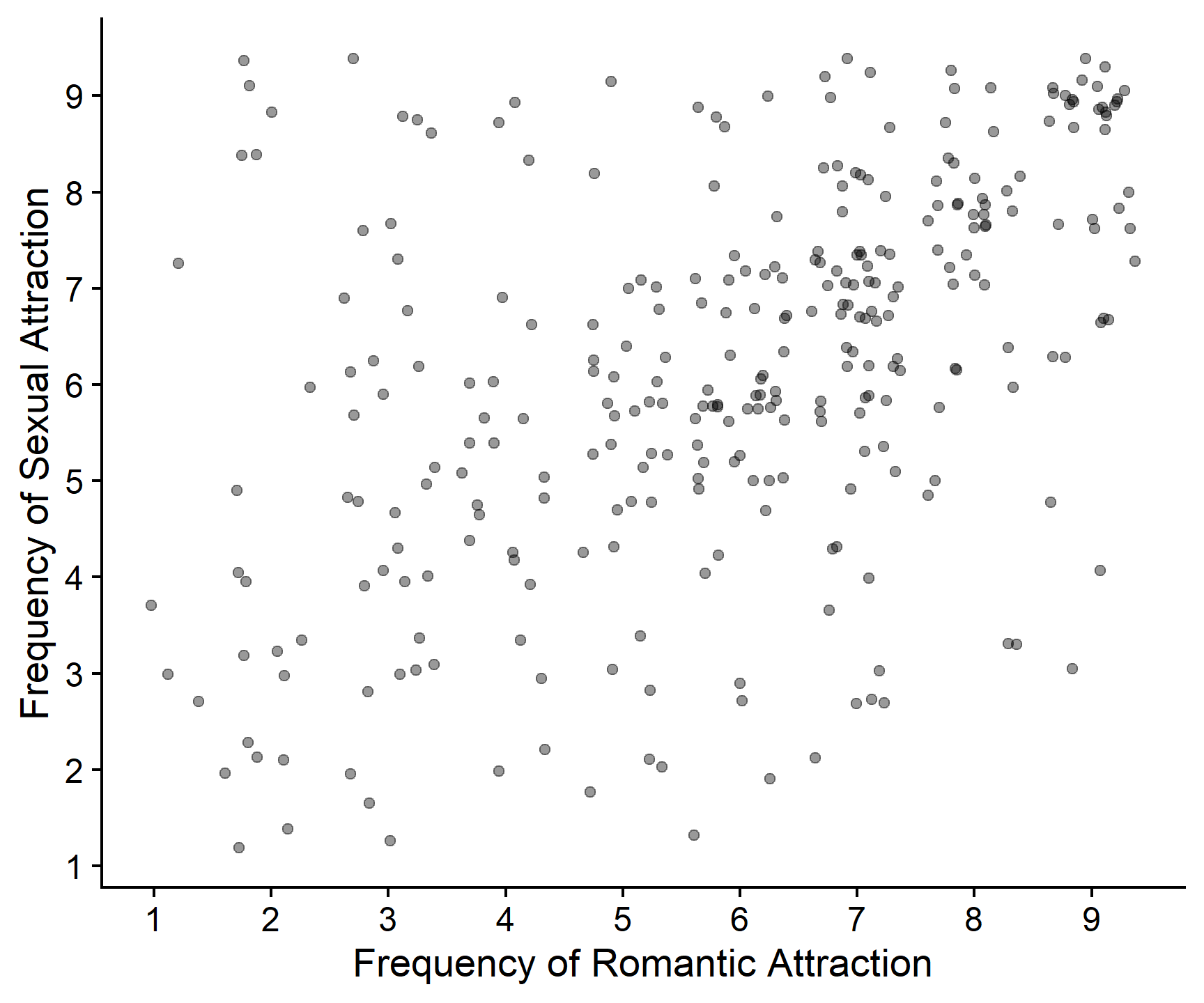
Create a scatterplot of the same variables, with romantic_freq on the x axis and sexual_freq on the y axis, and tweak the formatting to make it look professional.

gensex %>% 
  ggplot(aes(x = romantic_freq, y = sexual_freq)) +
  geom_point(position = "jitter", alpha = .4) +
  scale_x_continuous(name = "Frequency of Romantic Attraction",
                     breaks = c(0:9)) +
  scale_y_continuous(name = "Frequency of Sexual Attraction",
                     breaks = c(0:9)) +
  cowplot::theme_cowplot()

Task 10.1jazz...

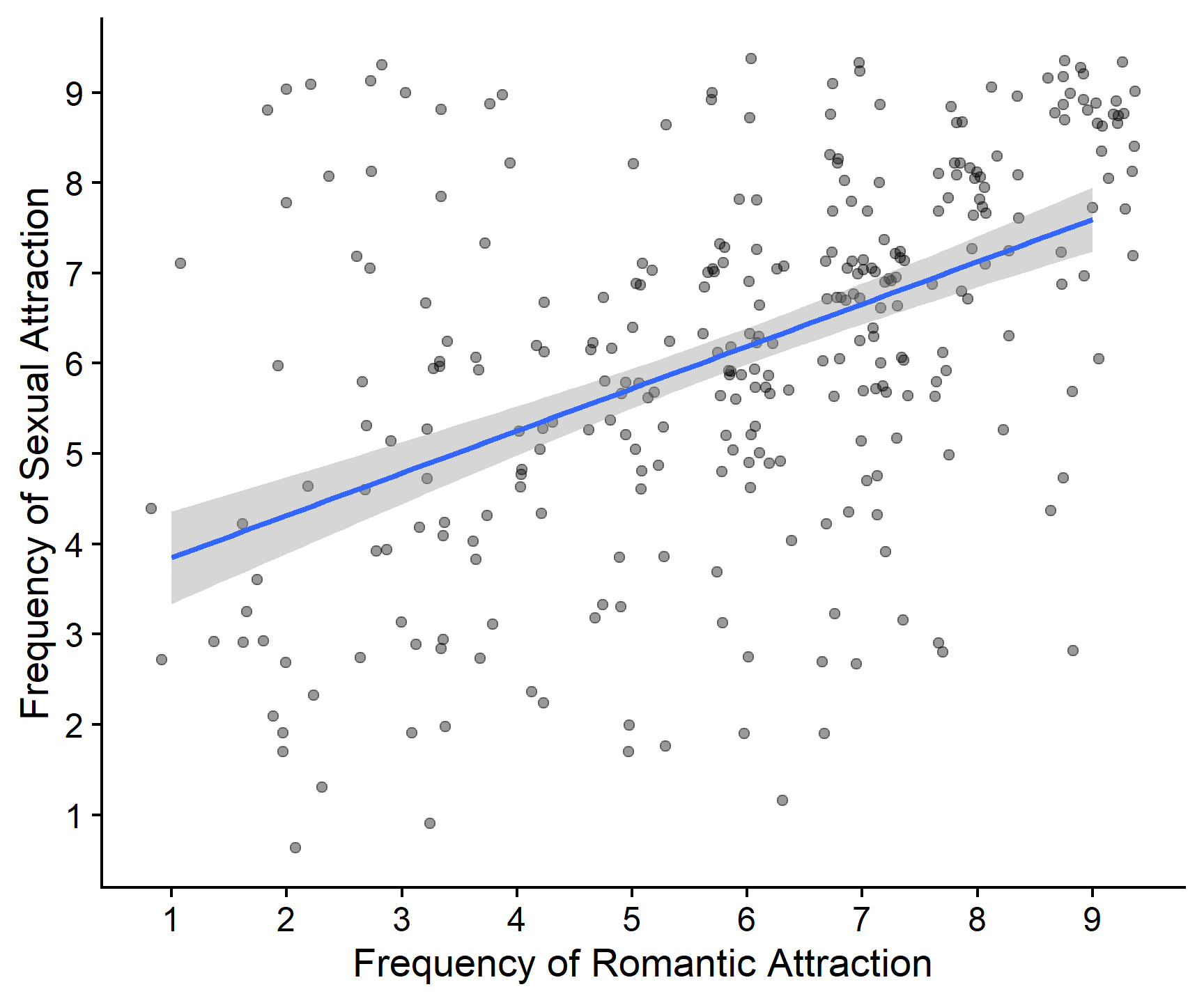
Optionally, figure out how to add a line of best fit to this plot. Does it look like you expected based on the visualisation?

gensex %>% 
  ggplot(aes(x = romantic_freq, y = sexual_freq)) +
  geom_point(position = "jitter", alpha = .4) +
  scale_x_continuous(name = "Frequency of Romantic Attraction",
                     breaks = c(0:9)) +
  scale_y_continuous(name = "Frequency of Sexual Attraction",
                     breaks = c(0:9)) +
  geom_smooth(method = "lm", formula = y~x) +
  cowplot::theme_cowplot()

Task 12Prog-rocK

Overall, what have we discovered about the relationship between the frequency of sexual and romantic attraction? What don’t we know yet? Write down your thoughts in your Markdown.

Recap

Well done on all of your hard work! Make sure you work on these ideas and get them down clearly; they will be very important for the rest of the module. You should now be able to do the following:

• Understand how the b₀ (intercept) and b₁ (slope) values specify the line
  • Explain why a b₁ value of 0 represents no relationship between the predictor and the outcome
• Create a linear model using lm()
• Write an equation for the linear model using lm() output
• Use the equation to calculate a predicted value for the outcome, given a value of the predictor.

Good job!

That’s all for today. See you soon!